Reële getallen

Waar gaat het over?

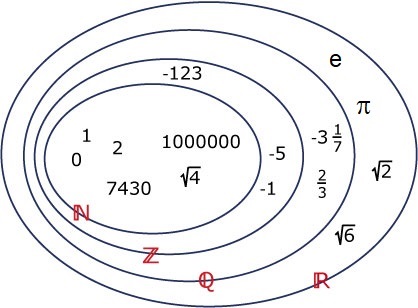
In het tientallig stelsel kun je duidelijk soorten getallen onderscheiden met verschillende eigenschappen. Bekend zijn de gehele getallen, die bestaan uit positieve en negatieve getallen en `0`. Daarnaast zijn er rationale getallen, de breuken die in het tientallig stelsel ook cijfers achter de komma hebben, soms oneindig veel, maar altijd met herhaling. En tenslotte zijn er getallen die een oneindig aantal zich niet herhalende decimalen hebben, die zijn alleen te benaderen.

Hoe werkt het?

De getallen `NN = {0, 1, 2, 3, ...}` zijn de natuurlijke getallen.
Door daar `{text(-)1, text(-)2, text(-)3, ...}` aan toe te voegen krijg je de gehele getallen.
Alle getallen die als breuk zijn te schrijven vormen de rationale getallen `QQ` (ratio = verhouding), dus ook de gehele getallen.
Alle getallen die je niet als breuk kunt schrijven vormen de irrationale getallen.
De rationale en de irrationale getallen samen zijn de reële getallen `RR`.

Wie en wanneer?

Heel lang kende de mensheid alleen natuurlijke getallen, zelfs `0` bestond als zodanig niet. En daarnaast werd er gerekend met verhoudingen van twee natuurlijke getallen, de breuken.
Steeds werd gedacht dat dit alle mogelijke getallen waren. Tot de Oude Grieken er (vanwege de stelling van Pythagoras) achter kwamen, dat de hypotenusa van een rechthoekig driehoekje met rechthoekszijden van `1` (lengte `sqrt(2)`) niet als een breuk te schrijven was.
Lees voor een bewijs dat `sqrt(2)` irrationaal is dit artikel.