Verhoudingen en breuken
Waar gaat het over?
Wil je met 7 personen 3 broden eerlijk verdelen, dan is de verhouding broden : mensen gelijk aan 3 : 7. Ieder 3 // 7 krijgt deel.
Dit laatste heet een breuk en je schrijft meestal 3/7.
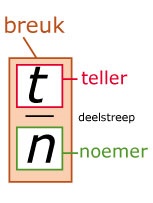
Omdat dit 3 zevende delen zijn, heet 7 de noemer (naamgever) van de breuk en is 3 de teller (het aantal zevende delen).
Tegenwoordig leert iedereen rekenen met breuken.
Hoe werkt het?
Allereerst zijn breuken met dezelfde verhouding gelijk: 3/7 = 6/14 = 9/21 = ...
Hiermee kun je breuken gelijknamig maken: 3/7 = 15/35 en 2/5 = 14/35.
Daarmee kun je ze optellen, aftrekken en delen:
3/7 + 2/5 = 15/35 + 14/35 = 19/35 en 3/7 - 2/5 = 15/35 - 14/35 = 1/35 en 3/7 // 2/5 = 15/35 // 14/35 = 15/14
Alleen vermenigvuldigen gaat anders: 3/7 * 2/5 betekent 3 keer éénzevende van 2/5, dus 3 keer 2/35 en dat is 6/35.
Wie en wanneer?
Al heel lang is de mens bekend met verhoudingen en dus met breuken. In het Oude Egypte werkte men vooral met stambreuken, breuken waarvan de teller 1 is, zie Rekenen in het Oude Egypte. En de Babyloniërs hadden in verband met hun zestigtallig stelsel weer een eigen methode, zie Rekenen in Babylonië. De Oude Grieken namen deze methoden over, zie Rekenen met de Oude Grieken. Maar onze huidige technieken zijn pas na de invoering van de arabische/indiase cijfers en het het tientallig stelsel ontstaan. In Nederland is Willem Bartjens (1569 - 1638) via zijn rekenmethode "De Cyfferinge van Willem Bartjens Amstelredammer, inhoudende meest alle de Grondregelen der Cypherkonst. Seer nut en dienstelyck den Leerlingen ende alle liefhebberen der Konst." bekend.
Kernwoorden op deze pagina:
- getal
- cijfer
- gelijknamig