Oneindig
Waar gaat het over?
Oneindig kom je tegen als je door blijft tellen: `0, 1, 2, 3, 4, ...`.
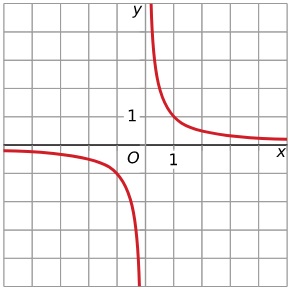
Maar ook bij grafieken zoals deze van de functie `y = 1/x`.
Kies je oneindig grote waarden dan zal deze functie het getal `0` benaderen. Hetzelfde geldt voor oneindig kleine (heel erg negatieve) waarden. Kies je daarentegen waarden vlak bij `0` dan worden juist de uitkomsten oneindig groot (positief of negatief).
Hoe werkt het?
Voor oneindig wordt het symbool `oo` gebruikt.
De natuurlijke getallen heten aftelbaar oneindig, er zijn er oneindig veel. Omdat de gehele getallen ook zo te tellen zijn (`0, 1, text(-)1, 2, text(-)2, 3, text(-)3, ...`) zijn ook die aftelbaar oneindig. Zelfs alle rationale getallen zijn zo te tellen, dus aftelbaar oneindig. Dergelijke verzameling getallen hebben telniveau `aleph_0`.
De reële getallen kun je zo niet tellen, die zijn overaftelbaar, telniveau `aleph_1`.
Bij grafieken gebruik je limieten om oneindigheid aan te geven: `lim_(x rarr oo) 1/x = 0` en `lim_(x darr 0) 1/x = oo`.
Wie en wanneer?
Het begrip limiet als grenswaarde werd voor het eerst gebruikt door Cauchy die zich bezighield met een nauwkeurige opzet van de analyse, de theorie van functies van één variabele. Door Euler werd het teken `oo` voor oneindig bedacht (een soort Möbiusband).
Eind 19e eeuw voerde Weierstrasz een nauwkeuriger definitie van het limietbegrip in.
Oneindigheid en aftelbaarheid werd pas voor het eerst bestudeerd door Cantor die de verzamelingenleer bedacht en de oneindigheid van sommige verzamelingen bestudeerde. Hij formuleerde de continuümhypothese: er bestaan geen oneindige verzamelingen met een telniveau (kardinaliteit) tussen `aleph_0` en `aleph_1` in. Deze hypothese is nog niet sluitend bewezen.
Kernwoorden op deze pagina:
- functie
- aftelbaar
- natuurlijke getallen
- gehele getallen
- rationale getallen
- reële getallen