Functies

Waar gaat het over?

Bij sommige verbanden tussen variabelen heeft er eentje een unieke uitkomst als je de andere weet. Die variabele is dan een functie van de andere (vaak met bijpassende formule).
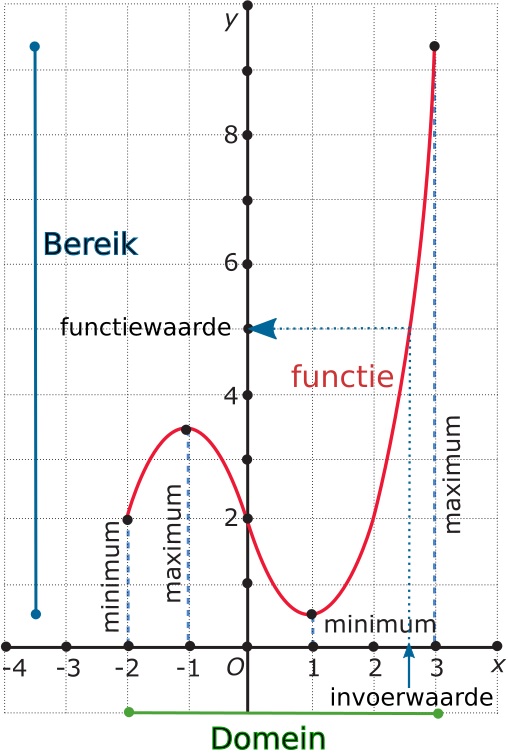
Als `y` een functie is van `x` hoort bij elke toegestane waarde van `x` precies één waarde van `y`.

Hoe werkt het?

Functies geef je vaak een naam: `y = text(fun)(x)` is een functie van één onafhankelijke variabele, de `x`. Je kunt er een grafiek bij maken in een `xy`-assenstelsel door een tabel te maken met `y`-waarden bij zelf gekozen `x`-waarden. De mogelijke `x`-waarden (invoerwaarden) vormen het domein, de bijbehorende `y`-waarden (functiewaarden) het bereik.
Er bestaan diverse standaardfuncties, zoals veeltermen, goniometrische functies, exponentiële- en logaritmische functies, en meer...
Er bestaan ook functies van meerdere variabelen zoals `z = text(fun)(x, y)` waarvan de grafieken (gekromde) oppervlakken zijn in een `xyz`-assenstelsel.

Wie en wanneer?

Pas rond 1600 werd het werken met formules en assenstelsels gangbaar. Daarna kwam vooral door Newton en Leibniz (die het woord "functio" - afkomstig van het Latijnse "fungor", een taak uitvoeren - voor het eerst gebruikte) het werken met functies in beeld. Een scherpe definitie bestond nog niet.

In de 18e en de 19e eeuw is de analyse ontwikkeld zoals je die nu op school leert. Er werden diverse notaties gebruikt, maar er was ook meer begrip nodig van de soorten getallen, van (deel)verzamelingen, van het werken met oneindigheden, enz. Veel wiskundigen in West-Europa waren hierbij betrokken.
Pas begin 19e eeuw gaf Johann Dirichlet de huidige definitie van het begrip functie.