Machten

Waar gaat het over?

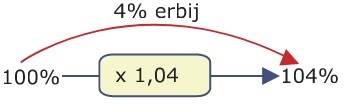
Soms neemt een hoeveelheid toe door steeds met hetzelfde getal te vermenigvuldigen. Bijvoorbeeld als je `4`% rente per jaar krijgt op €1000 spaargeld: als je verder niets doet en de rente blijft gelijk wordt het spaargeld elk jaar met groeifactor `1,04` vermenigvuldigt. Na vijf jaar heb je dan: `1000*1,04*1,04*1,04*1,04*1,04 = 1000*1,04^5~~1216,65`.
Die `1,04^5` heet de vijfde macht van `1,04`.

Hoe werkt het?

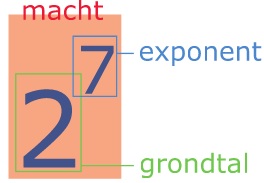
Voor het vermenigvuldigen met steeds hetzelfde getal gebruik je een macht met een grondtal en een exponent. Bijvoorbeeld:
`2*2*2*2*2*2*2 = 2^7`.
Reken je zo'n getal uit, dan wordt de uitkomst snel groot: `2^7 = 128`.
Je spreekt van machtsverheffen en je zegt "2 tot de macht 7" , of kortweg "2 tot de 7de" . Bij terugwerken vanuit een 7de macht gebruik je een 7de-machtswortel: `root[7](128)=2`.

Machten zijn vooral van belang bij exponentiële groei. Die komt voor bij groei en verspreiding van mensen, dieren, bacteriën, virussen, planten.

Wie en wanneer?

Het begrip macht is vermoedelijk al heel oud, maar de notatie voor machtsverheffen komt pas aan het begin van de zeventiende eeuw voor het eerst in geschriften voor. Onder andere René Descartes (1596 - 1650) gebruikte de notatie voor machten.
De Engelse wiskundige John Wallis (1616 - 1703) voerde ook negatieve en gebroken exponenten in.

In de 19de eeuw schreef Thomas Malthus voor het eerst over de exponentiële groei van het aantal mensen en wat dat voor ultieme gevolgen voor het leven op aarde kon hebben. In 1972 kwam het rapport "Grenzen aan de groei" van de Club van Rome uit, waarin de uitputtingsproblematiek van onze planeet verder werd uitgewerkt. Hopelijk zijn we wakker geworden...