Logaritmische schalen
Waar gaat het over?
Bij exponentiële groei heb je vaak grafieken waarbij de functiewaarden in het begin klein zijn, maar als snel heel groot worden. Om al die waarden toch in een grafiek te krijgen wordt op de verticale as een logaritmische schaal gebruikt. In plaats van het getal zelf wordt de logaritme van het getal uitgezet en het getal zelf op de as afgelezen.
Hoe werkt het?
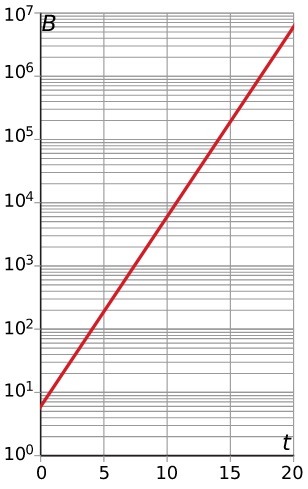
Je ziet hier de grafiek van `B = 6*2^t` met op de verticale as een logaritmische schaalverdeling.
De beginwaarde `6` is getekend op hoogte `log(6) ~~ 0,78` en omdat bij `t=10` geldt `B=6*2^10 = 6144` is die waarde getekend op hoogte `log(6144)~~3,79`. Op de verticale as kun je nu de juiste waarden alleen nog schatten.
Omdat er één as is met een logaritmische schaal, spreek je van een enkellogaritmisch assenstelsel. Exponentiële functies worden dan rechte lijnen. Heb je op beide assen een logarimische schaal, dan heb je dubbellogaritmisch papier en worden machtsfuncties rechte lijnen. Op een logaritmische schaal komen geen nul en geen negatieve getallen voor.
Wie en wanneer?
Nadat John Napier (1550 - 1617) samen met Henry Briggs (1561 - 1630) de logaritmen met grondtal `10` had bedacht, ontwikkelde Edmund Gunter rond 1620 in Oxford de logaritmische schaalverdeling.
Op basis daarvan ontwierp William Oughtred (1574 - 1660) de eerste rekenliniaal, die bestond uit twee langs elkaar glijdende logaritmische schalen. Daarmee is tot de opkomst van de elektronische rekenapparatuur het vermenigvuldigen en delen van getallen uitgevoerd. Het apparaat werd tot in de jaren '70 van de vorige eeuw gebruikt.

Kernwoorden op deze pagina:
- nul
- rekenmachine
- machtsfunctie