Logaritmen

Waar gaat het over?

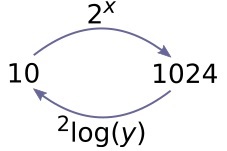
Als een hoeveelheid begint met `1` en groeit met groeifactor (grondtal) `2` per tijdseenheid, dan wil je soms weten wanneer deze explosieve groei boven de `50text(.)000` uitkomt.
Je lost dan de vergelijking `2^t = 50text(.)000` op.
De oplossing van zo'n vergelijking is een logaritme: `t = \ ^2log(50text(.)000)`.
Met een logaritmentabel of (zoals nu) met een rekenmachine vind je `t ~~ 15,61` tijdseenheden.

Hoe werkt het?

Om met logaritmen te werken kun je rekenregels afleiden:

`\ ^glog(a) = (log(a))/(log(g))` waarin `log(a)` en `log(g)` logaritmen met grondtal `10` zijn.

`\ ^glog(a*b) = \ ^glog(a) + \ ^glog(b)` en `\ ^glog(a/b) = \ ^glog(a) - \ ^glog(b)`

Met deze laatste twee regels kun je van een vermenigvuldiging een optelling van logaritmen maken.

Wie en wanneer?

De Schot John Napier (1550 - 1617) hield zich bezig met methoden om het rekenen met grote getallen te vergemakkelijken. Daartoe vond hij de logaritmen en de rekenregels voor logaritmen uit. Samen met Henry Briggs (1561 - 1630) ontwikkelde hij de logaritmen tot een krachtig rekeninstrument met een vast grondtal, namelijk `10`.

Zelf had Napier logaritmen bedacht met het grondtal `text(e)`, dat zijn de zogenaamde natuurlljke logaritmen (of neperse logaritmen): `\ ^text(e)log(a) = ln(a)`.
Het getal `text(e) = 2,71828...` is later genoemd naar de beroemde wiskundige Euler die de eigenschappen van dit getal verder heeft onderzocht.