Veeltermen

Waar gaat het over?

Een veelterm - of polynoom - is een uitdrukking van de vorm `a_n x^n + a_(n-1) x^(n-1) + ... + a_0`, waarin `n` een natuurlijk getal is. Functies die de vorm van een veelterm heten `n`degraads functies en zijn veel onderzocht, denk maar aan de eerstegraads (lineaire) en de tweedegraads (kwadratische) functies. Vaak wordt dan gezocht naar nulpunten en extremen.

Hoe werkt het?

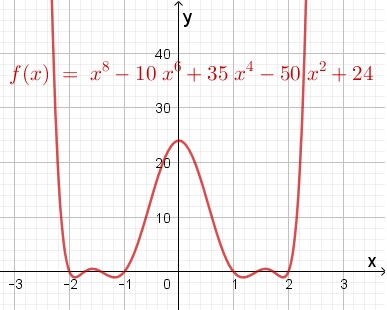
Hier zie een achtstegraads functie. Er zijn precies `8` nulpunten, de functie is te schrijven als `f(x) = (x-1)(x+1)(x-sqrt(2))(x + sqrt(2))(x-sqrt(3))(x+sqrt(3))(x-2)(x+2)`.
Heel lang is gezocht naar manieren om alle veeltermfuncties in dergelijke factoren te ontbinden. Bij kwadratische functies bijvoorbeeld werd de `abc`-formule ontdekt om de twee nulpunten (soms complexe getallen) te vinden. Bij derdegraads en vierdegraads functies werd iets vergelijkbaars gevonden. Maar daarmee hield het op: er werd ontdekt dat vanaf vijfdegraads functies zoiets niet meer mogelijk was.

Wie en wanneer?

Met name Italiaanse wiskundigen als Tartaglia (1449 - 1557), Cardano (1501 - 1576) hebben het oplossen van derdegraads en vierdegraads vergelijkingen bestudeerd. Ze slaagden er in om er procedures voor te ontwikkelen.
Daarna werd dit natuurlijk doorgezet naar vijfdegraads vergelijkingen, tot de Noor Niels Henrik Abel (1802 - 1829) bewees dat dit niet mogelijk was met behulp van wortelvormen binnen de reële getallen. Wel was al begin 17e eeuw aangenomen dat elke veeltermfunctie van de `n`de graad precies `n` nulpunten heeft, maar dat geldt alleen binnen de complexe getallen. Deze hoofdstelling van de algebra is pas begin 19e eeuw bewezen m.b.v. functietheorie. Er bestaat geen zuiver algebraïsch bewijs.