Statistiek met OO-Calc: Data presenteren
Een frequentietabel maken
Open jouw bestand Stat[...].ods.
Als het goed is tref je de gegevens van 154 leerlingen in 4 havo aan. Er zijn gegevens van 11 statistische variabelen verzameld. Op het werkblad wordt omschreven wat onder elke variabele wordt verstaan.
Je wilt de lengtes van jongens en meisjes vergelijken om de verschillen tussen beide deelgroepen te kunnen bekijken. Je maakt dan frequentietabellen en histogrammen voor beide groepen afzonderlijk. Maak eerst een nieuw werkblad met alleen de variabelen waarmee je wilt werken. Dat doe je zo:
- Kopieer eerst het werkblad naar een nieuw werkblad door onderaan met de rechter muisknop op de naam van het eerste werkblad te klikken en "Blad verplaatsen/kopiëren" te kiezen.
Vink dan "Kopiëren" aan en OK. - Je hebt een kopie gemaakt van het originele werkblad. Wijzig de naam van dit werkblad in "LengteGewichtJM" door met de rechter muisknop op de naam te klikken en "Bladnaam wijzigen" te kiezen.
- Vervolgens haal je de kolommen gebjaar, gebmnd, cijfgem, cijfwis, huiswerk, wisgroep, profiel en plezier weg, door deze kolommen in de balk met de letters van de cellen tegelijk te selecteren en met behulp van de rechter muisknop te verwijderen.
De kolommen gewicht en lengte worden nu D en E. Verwijder ook de uitleg over de betekenis van de variabelen om ruimte te maken voor je gegevensanalyse.
Je hebt nu een werkblad om te werken met geslacht, lengte en gewicht.
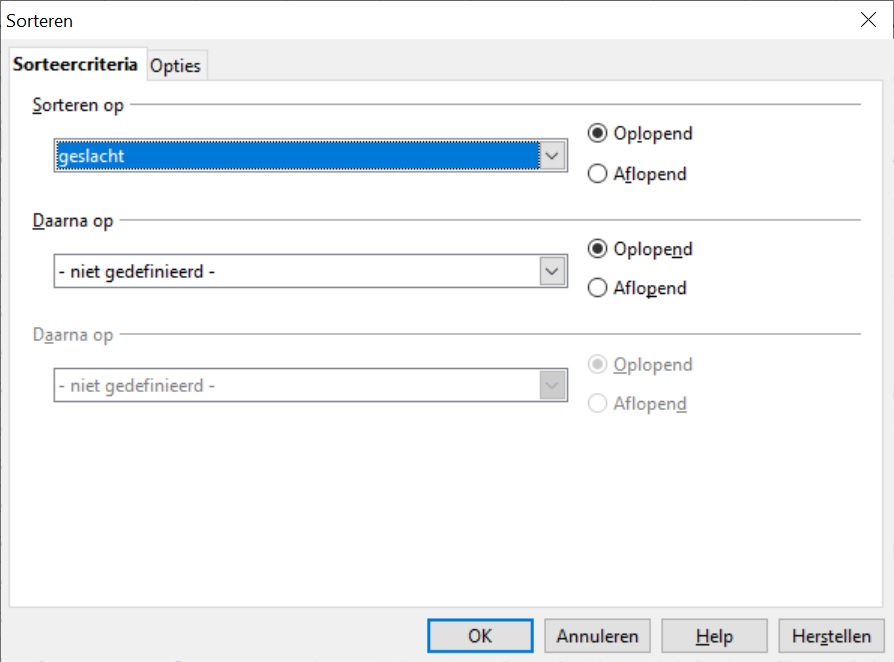
- Sorteer de gegevens zo, dat de jongens bij elkaar staan en de meisjes bij elkaar staan.
- Selecteer de kolom "geslacht" door op de letter bovenaan deze kolom te klikken.
- Kies op bij "Gegevens" voor "Sorteren" en "Selectie uitbreiden" en je krijgt het dialoogscherm hiernaast.
- Kies "Aflopend" en dan OK. - Ga na dat alle jongens bovenaan staan. Hoe zou je de meisjes bovenaan hebben gekregen?
Sla steeds tussentijds je resultaten op!
Nu wil je overzichtelijke frequentietabellen en diagrammen maken om te kunnen vergelijken. Daartoe maak je een geschikte klassenindeling, van ongeveer 10 klassen. Excel kan een bijpassende frequentietabel voor je maken. Daarmee wordt het vervelende "turven" overbodig.
Je doet dit eerst voor de variabele lengte. Zo maak je een overzicht van de kleinste en de grootste lengtes.
- Zet in de cellen G2, H2 en I2 achtereenvolgens "lengte", "jongens", "meisjes". En zet in de cellen G3 en G4 "minimum" en "maximum".
- Zet in cel H3: =MIN(E2:E70) en [ENTER].
Je kunt dit doen door te beginnen met =MIN( en dan de lengtes van de jongens te selecteren (cellen E2 t/m E70). Dan ) en [ENTER]. - Zet in de cellen H4, I3 en I4 de andere maximale en minimale lengtes.
Je weet nu welke verschillende lengtes er voorkomen. Als het goed is lopen ze vanaf 156 tot en met 200. Daarmee maak je een klassenindeling, bijvoorbeeld 156 t/m 160, 161 t/m 165, etc.
- Zet in G6 het woord "klassen" en voer in cel G7 t/m G17 de klassen 150-<155, 155-<160, 160-<165, etc, in.
- Zet in H6 het woord "max" en voer in cel H7 t/m H17 de maximale lengtes van de klasse in. Zet in H7 155 en in H8 160 en selecteer H7 en H8. Sleep met de vulgreep tot je een kolom hebt met lengtes van 155 t/m 205 (205 staat in cel H17).
- Selecteer de cellen I7 t/m I17 en voer in de functiebalk =INTERVAL(E2:E70;G7:G53) en doe [Ctrl][Shift][Enter].
- Je krijgt dan in kolom I een frequentieverdeling van de lengtes van de jongens. In bijvoorbeeld cel I12 zie je dat er 22 jongens zijn met een lengte vanaf 176 t/m 180 cm.
- Doe dit zelf ook voor de lengtes van de meisjes in de kolom J. Om de lengtes van beide groepen te kunnen vergelijken is het wel verstandig om dezelfde beginwaarden voor de klassengrenzen en de klassenbreedte te kiezen.
- Controleer je aantallen door I7 t/m I17 en J7 t/m J17 op te tellen: 69 jongens en 85 meisjes.
Je hebt nu nette frequentietabellen voor de lengtes van de 154 leerlingen.
Wil je liever relatieve frequentietabellen?
Je moet dan elke frequentie delen door het totaal en (om procenten te krijgen) vermenigvuldigen met 100.
Sla weer je werkmap op!
- Voer dit alles nog eens uit voor de variabele gewicht, zowel voor de jongens als de meisjes.
Diagrammen om verschillen te zien
Diagrammen kun je maken op het tabblad "Invoegen". Een histogram voor de lengtes van de jongens gaat zo:
- Selecteer de gemaakte frequentietabel voor de jongens (hier: J7 t/m J17) in één keer.
- Kies bij Invoegen > Diagram voor het staafdiagram (dus voor "Kolom") en je krijgt na [Voltooien] een staafdiagram te zien.
- Om bij de horizontale as de klassenindeling te krijgen klik je met de rechter muisknop op het diagram en kies je "Bewerken". Vervolgens rechtsklik je nogmaals op het diagram en kies je "Gegevensbereiken". Je krijgt dan een dialoogvenster waarin je via "Gegevensreeksen" op de horizontale as de aslabels kunt toevoegen. Daarvoor gebruik je de klassen in kolom G. Met het knopje rechts naast "Categorieën" kun je die selecteren en dan komen ze bij de figuur te staan.
- Mooi wordt dit pas als je de as beter opmaakt. Dat doe je door te rechtsklikken op de as en "As opmaken". Daar kun je bij "Label" de aslabels 90^@ draaien.
- Dan is het nog niet helemaal klaar, want de staven moeten bij een histogram tegen elkaar aanzitten. Dat bereik je door met de rechter muisknop op een staaf te klikken en dan te kiezen voor "Gegevensreeksen opmaken". Daar kun je bij "Opties" de afstand tussen de kolommen op bijna 0% zetten.
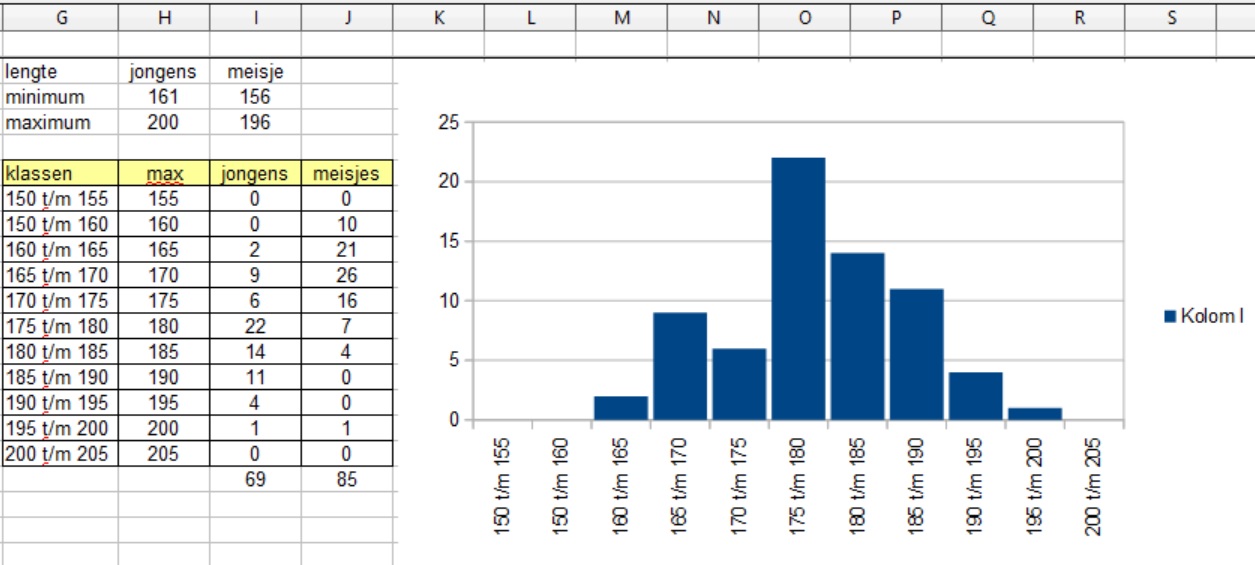
Als het goed is krijg je een histogram zoals dat hierboven te zien.
Je hebt natuurlijk wel gezien dat je ook achteraf de grafiek kunt opmaken door met je rechter muisknop de verschillende gedeelten van de grafiek te selecteren. En je kunt ook andere soorten diagrammen maken. Experimenteer maar even. Als je jongens en meisjes op deze manier wilt vergelijken, moet je met relatieve frequenties werken.
- Maak in dit werkblad een lijngram voor de lengteverdeling van de meisjes. Maak alles zo fraai mogelijk en sla het resultaat op.
- Vergelijk de lengteverdeling van de jongens en de meisjes met behulp van staafdiagrammen van de relatieve frequenties. Maak alles zo fraai mogelijk en sla het resultaat op.
- Voer alles nog eens uit voor de variabele gewicht, zowel voor de jongens als de meisjes.
De statistische functies
Je kunt eenvoudig alle centrum en spreidingsmaten door OO-Calc laten berekenen. Dat doe je zoveel mogelijk vanuit de ruwe data! Hieronder zie je hoe je in een zelf gekozen cel de centrum- en de spreidingsmaten van de lengtes van de jongens bepaalt:
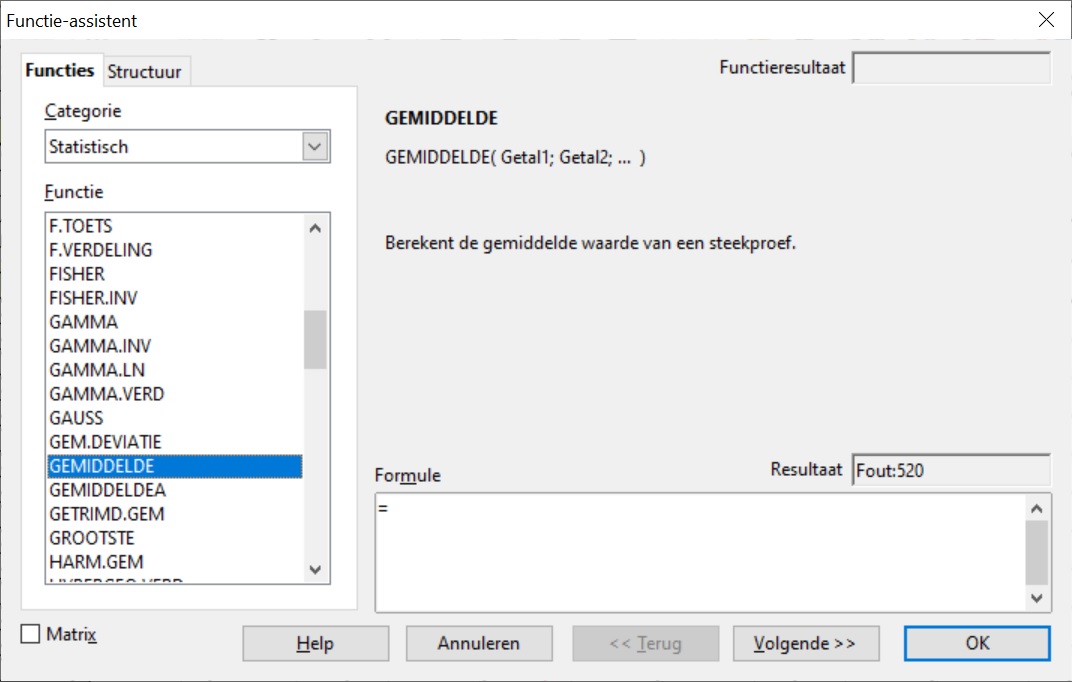
- de modus wordt berekend met =MODUS(E2:E70)
- de mediaan wordt berekend met =MEDIAAN(E2:E70)
- het gemiddelde wordt berekend met =GEMIDDELDE(E2:E70)
- de standaardafwijking wordt berekend met =STDEVP(E2:E70)
- de kleinste waarneming wordt berekend met =MIN(E2:E70)
- de grootste waarneming wordt berekend met =MAX(E2:E70)
- de spreidingsbreedte wordt berekend met =MAX(E2:E70)-MIN(E2:E70)
- het eerste kwartiel Q1 wordt berekend met =KWARTIEL(E2:E70;1)
- het derde kwartiel Q2 wordt berekend met =KWARTIEL(E2:E70;3)
- de kwartielafstand wordt berekend door de kwartielen van elkaar af te trekken
MODUS, MEDIAAN, e.d. zijn statistische functies in OO-Calc. Je kunt gewoon hun naam na het = teken invoeren in de cel, maar je kunt ze ook vinden met de knop: f_X op de bovenbalk of in het menu bij Invoegen > Functie. Als je daarop drukt wordt de wizard functies ingeschakeld. Kies in het venster dat nu verschijnt "Statistisch" en je vindt de hele lijst met statistische functies. Zoek daarin de juiste functie en klik daarop. Je krijgt nu een venster te zien, waarin je kunt invoeren: E2:E70. Dat zijn de cellen waarin de waarnemingen staan. (Je kunt die cellen ook met de muis selecteren.) Kies [OK] en je vindt de juiste waarde in de gewenste cel.
- Bepaal van de jongens al deze centrummaten en spreidingsmaten.
- Doe ditzelfde bij de lengtes van de meisjes.
- Ga na, dat al de berekende statistische maten mee veranderen als je lengtes en/of gewichten in de tabel verandert.
Boxplots maken
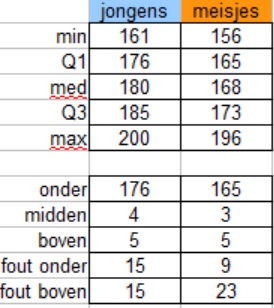 Om de lengtes van jongens en meisjes met elkaar te vergelijken kun je boxplots maken. In OO-Calc heb je eerst een paar gegevens nodig om ze te maken. Je moet de twee kwartielen, het minimum en het maximum van de gegeven waarden en de twee medianen bepalen. Dat laat je OO-Calc in een tabel zetten zoals die je hiernaast ziet.
Om de lengtes van jongens en meisjes met elkaar te vergelijken kun je boxplots maken. In OO-Calc heb je eerst een paar gegevens nodig om ze te maken. Je moet de twee kwartielen, het minimum en het maximum van de gegeven waarden en de twee medianen bepalen. Dat laat je OO-Calc in een tabel zetten zoals die je hiernaast ziet.
Omdat OO-Calc geen boxplot optie kent, ga je een gestapeld staafdiagram ombouwen tot een boxplot. De box wordt begrensd door de ondergrens Q1 en de bovengrens Q3. Het middelste getal is de mediaan. Het gestapelde staafdiagram bestaat nu uit drie blokken: het eerste blok is vanaf 0 tot "onder" = Q1, het tweede blok loopt van "onder" tot "midden" = Mediaan - Q1 en het derde blok loopt van "midden" tot "boven" = Q3 - Mediaan.
De twee "snorharen" ("whiskers") van de boxplot maak je met behulp van foutbalken: fout onder = Q1 - minimum en fout boven = maximum - Q3. Nu ga je als volgt te werk:
- Maak eerst deze tabel naast je gegevens, voor de jongens en de meisjes naast elkaar zoals je hier ziet.
- Selecteer nu de waarden van onder, midden, boven en fout onder in één keer.
- Ga naar Invoegen > Diagram en kies als diagram een gestapeld staafdiagram (tweede staafdiagram). Kies [Volgende] en "Gegevensreeksen in rijen". Kies [Volgende] en kies bij "Categorieën" de cellen H2:I2. Kies [Voltooien].
- Wat je nu krijgt lijkt nog niet op een staafdiagram. Daarvoor moet je het diagram selecteren en met rechtsklikken voor "Bewerken" kiezen.
- Kies eerst de onderste gegevensreeks door op één van die blokken te rechtsklikken en "Y-foutbalken invoegen" te kiezen. Zet "Celbereik" en "Negatief" aan en kies de cellen H12:I12. Je krijgt een foutbalk te zien in de onderste gegevensreeks. Rechtsklik nog eens op die gegevensreeks en zet bij "Gegevensreeksen opmaken" de opvulling uit.
- Rechtsklik op de bovenste blokken en kies "Y-foutbalken invoegen". Zet "Celbereik" en "Positief" aan en kies de cellen H13:I13. Je krijgt de bovenste foutbalk te zien.
Je hebt nu twee verticale boxplots naast elkaar. Waarschijnlijk wil je de assen nog aanpassen (waarden van 150 tot 210 zijn op de horizontale as wel genoeg). En wellicht wil je de boxplots nog van kleuren voorzien. Ga vooral je gang.
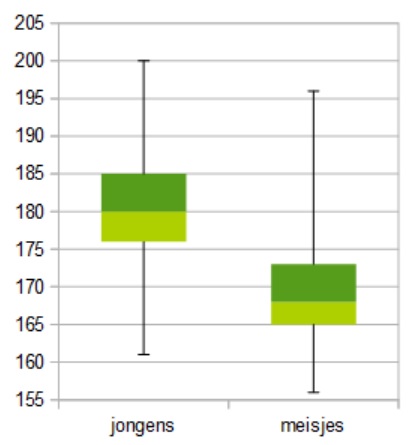
Ga na, dat al de berekende statistische maten mee veranderen als je een lengtes en/of gewichten in de tabel verandert. Het uitbreiden van de tabel is ook niet al te moeilijk, je hoeft dan maar een kleine aanpassing in de formules aan te brengen.
Sla je resultaten op!
- Voer dit alles nog eens uit voor de variabele gewicht, zowel voor de jongens als de meisjes. Maak voor dit geval verticale boxplots.
Cumulatieve frequenties
Stel je wilt de frequentietabellen van de lengtes van jongens en meisjes vergelijken met behulp van cumulatieve frequentiepolygonen.
- Je hebt eerder gewerkt in het werkblad "LengteGewichtJM". Kopieer dit werkblad naar "LengteGewichtJM_2".
- Maak op dit werkblad voor de jongens een frequentietabel in de cellen I7 t/m I17.
- Maak in de cellen J7 t/m J17 de somfrequenties (cumulatieve frequenties.
Zet in J7 =$I7 en zet in J8: =$J7+$I8. Kopieer dit naar beneden t/m J17. - Maak in de cellen K7 t/m K17 de relatieve somfrequenties (cumulatieve frequenties.
Zet in K7 =$J7/$I$18*100 en kopieer dit naar beneden t/m K17. - Doe hetzelfde voor de meisjes.
- Je maakt nu de twee cumulatieve relatieve frequentiepolygonen in één figuur.
- Selecteer de relatieve somfrequenties in K7 t/m K17 en N7 t/m N17 en kies bij "Invoegen > Diagram" voor "Lijndiagram" en als Subtype het lijndiagram met zichtbare punten en lijnen.
- Verander de aslabels van de horizontale as in de correcte lengteklassen en zet bijschriften bij de assen. Pas ook de namen in de legenda aan.
Als het goed is krijg je deze figuur:
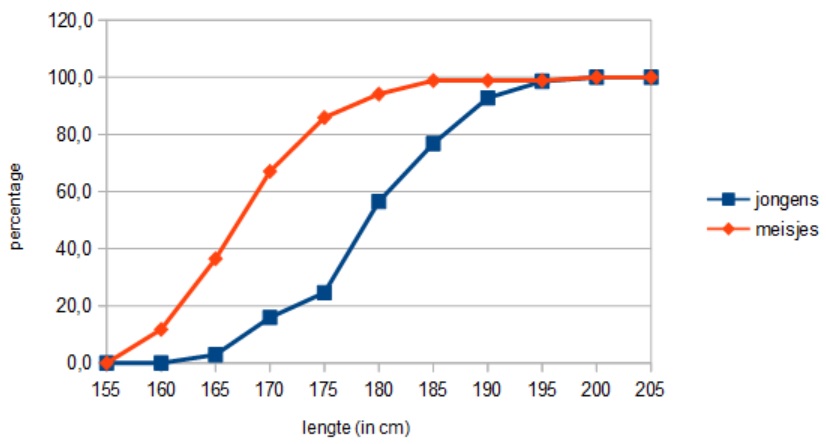
Stel je wilt verdeling van de wiskundecijfers per profiel (CM, EM, NG en NT) bekijken. Deze vier frequentieverdelingen wil je vergelijken. Maak eerst een nieuw werkblad met de variabelen geslacht, cijfwis en profiel.
In dat werkblad ga je dan zo te werk:
- Sorteer alle gegevens op de variabele profiel.
- Maak frequentietabellen van cijfwis per profiel. Zet ze om naar relatieve frequenties en maak er histogrammen bij.
- Maak ook cumulatieve relatieve frequentiepolygonen per profiel.
Je hebt nu geleerd om cumulatieve frequentiepolygonen te maken.
- Voer dit alles nog eens uit voor de variabele gewicht, zowel voor de jongens als de meisjes.
Het practicum afsluiten
Gebruik het bestand met gegevens van 154 leerlingen en probeer elk van de volgende vragen te beantwoorden met behulp van tabellen, diagrammen, centrummaten en spreidingsmaten. Bekijk daarbij goed in je wiskundeboek welke tabellen, diagrammen, centrummaten en spreidingsmaten zinvol zijn in de genoemde situaties. Motiveer het gebruik van de juiste diagrammen en maten.
- Zijn er duidelijke verschillen in gewicht tussen de meisjes en de jongens van deze groep leerlingen? Motiveer je antwoord m.b.v. histogrammen en gemiddelde en spreiding.
- Zijn er duidelijke verschillen in gewicht tussen de meisjes en de jongens van deze groep leerlingen? Motiveer je antwoord m.b.v. boxplots.
- Hebben de leerlingen in de N-profielen hogere cijfers in 3 havo gehad dan de leerlingen in de M-profielen? Motiveer je antwoord m.b.v. diagrammen en bijpassende centrummaten en spreidingsmaten.
- Formuleer zelf een vraag waarin je de verschillen tussen twee deelgroepen aan de orde stelt. Beantwoord je vraag m.b.v. diagrammen en bijpassende centrummaten en spreidingsmaten.
![]() Math4all
Math4all

