Rekentaak 8: Grafieken en verbanden

In deze rekentaak mag je met rekenmachine werken! Het gaat hier om het herkennen van de juiste rekenacties binnen context...

 

Inhoud:

 

Grafieken

Bestudeer eerst:

 

LogoM4Ainf.gif www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Verbanden

www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Formules

 

 

Opgaven

 

  1. Zinnen zoals hieronder kom je bijna dagelijks tegen.
    • A - Hoe meer uur je werkt, hoe meer je verdient.
    • B - Hoe langer je slaapt, hoe beter je bent uitgerust.
    • C - Hoe langer je fietst, hoe dichter je bij huis komt.
    • D - Hoe meer uur je televisie kijkt, hoe minder uur je aan je huiswerk kunt besteden.
    Elk van deze zinnen geeft een verband tussen twee variabelen weer.
    1. Schrijf telkens de twee variabelen op.
    2. Je kunt telkens het verband weergeven in een grafiek. Geef aan of die grafiek stijgend of dalend is.

  2. Een auto rijdt met één liter benzine (gemiddeld) `15` km.
    1. Welke formule hoort bij het verband tussen hoeveelheid benzine en gereden afstand?
    2. Maak een tabel van de hoeveelheid benzine bij gereden afstanden van `10, 20, 30, 40` en `50` km.
    3. Bij het verband wordt een grafiek gemaakt. Is de grafiek een rechte lijn? Gaat de grafiek door de oorsprong?
    4. Hoeveel liter benzine heb je nodig om `337,5` km te rijden?

  3. Van een rechthoek is de oppervlakte `600` m2.
    1. Bereken de lengte van de rechthoek als de breedte `15` m is.
    2. Hoe breed is de rechthoek als de lengte `120` m is?
    3. Geef een formule die het verband tussen de lengte en de breedte van deze rechthoek weergeeft.
    4. De grafiek bij dit verband is geen rechte lijn. Schets die grafiek.

  4. Twee taxibedrijven berekenen hun prijs op verschillende manieren:
    Bij bedrijf A hoort de formule: `text(prijs) = 2 * text(aantal km) + 2`.
    Bij bedrijf B hoort de formule: `text(prijs) = 1,5 * text(aantal km) + 5`.
    1. Welk bedrijf is het goedkoopst als je een rit van `3` km maakt?
    2. Welk bedrijf is het goedkoopst bij een rit van `10` km?
    3. Bij welk aantal gereden km zijn beide bedrijven even duur?

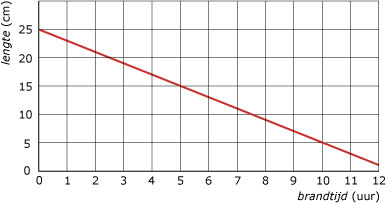  5. RT08-01.jpg Hoe langer een kaars brandt, hoe korter hij wordt. Er is een verband tussen de brandtijd en de lengte van een cilindervormige kaars. Bij dit verband is een grafiek getekend. De grafiek gaat door `(0, 25)` en `(10, 5)`
    1. Hoeveel cm wordt deze kaars elk uur korter?
    2. Hoe lang is de kaars na `3` uur branden precies?
    3. Na hoeveel uur is de kaars op?

Bestudeer vervolgens:

 

www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Formule naar grafiek

 

 

Opgaven

 

  1. Hoveniersbedrijf Jongman rekent voor het winterklaar maken van een tuin € 75,- plus € 4,- per m2.
    1. Maak een formule bij het verband tussen oppervlakte en tuinkosten.
    2. Maak een tabel bij deze formule. Neem oppervlaktes van `0, 50, 100, 150, 200` m2.
    3. Maak een bijpassende grafiek.
    4. Meneer Van Gils heeft zijn tuin laten opknappen. Hij kreeg een rekening van € 475,-. Hoe groot is de tuin van meneer Van Gils.

  2. Een aannemer krijgt de opdracht een kantoor te bouwen. De opdracht betekent `24000` manuren werk. Dit betekent dat als één man al het werk zou doen, hij er `24000` uur mee bezig zou zijn. Natuurlijk wordt een kantoor niet door één persoon gebouwd.
    1. Stel dat er `20` mensen aan het kantoor werken. Hoeveel uur is ieder dan gemiddeld aan het werk?
    2. Hoeveel uur werkt iedere werknemer gemiddeld als er `100` werknemers aan het kantoor werken? In hoeveel weken van `40` uur kan het dan gebouwd worden?
    3. Er is een verband tussen het aantal werknemers dat aan de bouw werkt en het aantal uur per werknemer. Bij dat verband hoort de formule: `text(aantal uur per werknemer) = (24000)/(text(aantal werknemers))`.
      Maak een grafiek bij deze formule.
    4. De opdrachtgever wil dat de aannemer het kantoor in `3` maanden bouwt. Hoeveel werknemers moet de aannemer inzetten?

  3. Er is een verband tussen de lengte van je voet en je (Franse) schoenmaat. Als je de lengte (in cm) van je voet weet, kun je je schoenmaat als volgt berekenen: "Doe de lengte van je voet maal 1,5 en tel er dan nog 2 bij op."
    1. Stel een formule op bij dit verband.
    2. Maak een bijpassende grafiek.
    3. Welke voetlengte heeft iemand met schoenmaat 45?

 

resource.jpg

Recht evenredig en omgekeerd evenredig

Bestudeer eerst:

 

www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Recht evenredig

 

 

Opgaven

 

  1. Leg uit in welke van de volgende situaties sprake is van een recht evenredig verband.
    1. Uien betaal je per kg. Is de prijs van een hoeveelheid uien recht evenredig met het gewicht?
    2. Uien betaal je per kg. Is de prijs van een hoeveelheid uien recht evenredig met het aantal?
    3. Is de afgelegde weg recht evenredig met de tijd als je met een constante snelheid rijdt?
    4. Is de afgelegde weg recht evenredig met de tijd als een auto uit stilstand optrekt?
    5. Is de lengte van een rechthoek recht evenredig met de breedte als het gaat om gelijkvormige rechthoeken?
    6. Is de lengte van een rechthoek recht evenredig met de breedte als het gaat om rechthoeken met dezelfde omtrek?

  2. Loodvrije benzine kost € 1,42 per liter en je rijdt gemiddeld `1` op `12` (`1` L voor `12` km). Diesel kost € 1,10 per liter en je rijdt gemiddeld `1` op `20`. Het aantal km dat iemand in een jaar aflegt is `a`.
    1. Stel een formule op voor de brandstofkosten `K` van een auto die op loodvrije benzine rijdt.
    2. Stel een formule op voor de brandstofkosten `K` van een auto die op diesel rijdt.
    3. Een auto die op diesel rijdt is duurder in aanschaf en duurder in de wegenbelasting en de verzekering dan eenzelfde auto op benzine. Als dit betekent dat de auto op diesel per jaar `1400` euro duurder is, bij welk aantal km per jaar kun je dan beter een dieseluitvoering kopen?

  3. Een loodgieter berekent € 30,= aan voorrijkosten en per uur dat hij werkt €22,50.
    1. Leg uit waarom het verband tussen zijn arbeidsloon en het aantal gewerkte uren recht evenredig is.
    2. Leg uit waarom het verband tussen de totale kosten die hij in rekening brengt en het aantal gewerkte uren niet recht evenredig is.
    3. Welke formule geldt voor zijn totale kosten `TK` afhankelijk van het aantal gewerkte uren `u`?

  4. In een inkjetprinter gaan inktpatronen. Zo'n inktpatroon kost € 42,50. Je kunt er (gemiddeld) 500 afdrukken mee maken.
    1. Hoeveel ben je aan inkt kwijt als je `1800` afdrukken per jaar maakt?
    2. Met welke formule kun je de jaarlijkse kosten voor inkt berekenen?
    3. Zijn de jaarlijkse kosten voor inkt recht evenredig met het aantal afdrukken? Zo ja, wat is dan de evenredigheidsconstante?
    4. Zijn de jaarlijkse kosten voor het werken met deze printer ook recht evenredig met het aantal afdrukken? Licht je antwoord toe.

Bestudeer nu:

 

www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Omgekeerd evenredig

 

 

Opgaven

 

  1. Leg uit in welke van de volgende situaties sprake is van een omgekeerd evenredig verband.
    1. Je hebt 10 euro bij je. Is het aantal pennen dat je kunt kopen omgekeerd evenredig met de prijs per stuk?
    2. Is de afgelegde weg omgekeerd evenredig met de tijd als je met een constante snelheid rijdt?
    3. Is de de tijd die je nodig hebt om een bepaalde weg af te leggen omgekeerd evenredig met je snelheid?
    4. Is de lengte van een rechthoek omgekeerd evenredig met de breedte als het gaat om gelijkvormige rechthoeken?
    5. Is de lengte van een rechthoek omgekeerd evenredig met de breedte als het gaat om rechthoeken met dezelfde omtrek?
    6. Is de lengte van een rechthoek omgekeerd evenredig met de breedte als het gaat om rechthoeken met dezelfde oppervlakte?

  2. Een school zet voor gebruik door de leerlingen een kopieermachine neer. Die machine huurt de school voor € 650,- per maand. Elke kopie kost de school bovenop de huur van de machine nog eens `6` cent (papier en drukinkt). Per kopie heeft de school dus vaste kosten (`6` cent) en huurkosten.
    1. Leg uit waarom de huurkosten per kopie omgekeerd evenredig zijn met het aantal kopieën dat per maand met deze machine wordt gemaakt.
    2. Hoeveel bedragen de huurkosten als er `10000` kopieën per maand met deze machine worden gemaakt.
    3. De school wil de leerlingen `10` cent per kopie laten betalen. Hoeveel kopieën moeten er dan per maand minstens worden gemaakt opdat alle kosten worden terugverdiend?

  3. Je ziet hier vier grafieken. Bij welke van deze grafieken is sprake van een recht evenredig verband en bij welke van een omgekeerd evenredig verband? Geef in die gevallen de bijpassende formule.

    A  RT08-02.jpg    B  RT08-03.jpg    C  RT08-04.jpg    D  RT08-05.jpg

 

resource.jpg

Lineaire en exponentiële groei

Bestudeer eerst:

 

www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Lineaire verbanden

 

 

Opgaven

 

  1. Voor het verbruik van water betaal je twee soorten kosten:
    • een vast bedrag per jaar, het vastrecht;
    • een bedrag per m3 water die je verbruikt.
    Die bedragen kunnen per gebied verschillend zijn, afhankelijk van de leverancier van het water. In gebied A betaal je `36` euro vastrecht en `1,80` euro per verbruikte m3.
    1. Waarom is hier sprake van een lineair verband?
    2. Stel een formule op voor dit lineaire verband.
    3. In gebied B kost een waterverbruik van `100` m3 per jaar `203` euro en een waterverbruik van `200` m3 per jaar 358 euro. Hoeveel bedraagt daar het vastrecht als ook hier sprake is van een lineair verband?
    4. Stel een formule op voor het waterverbruik in gebied B.
    5. Bij welk waterverbruik ben je in beide gebieden even duur uit?

  2. RT08-06.jpg Zuiver cilindervormige kaarsen branden gelijkmatig op. Je ziet hier de grafieken van de lengte `L` (in cm) van twee van die kaarsen afhankelijk van de brandtijd `t` (in uur).
    1. Welke grafiek hoort bij de dikste kaars? Waarom?
    2. Waarom is er bij beide grafieken sprake van een lineair verband?
    3. Stel formules op voor het verband tussen `L` en `t`.
    4. Na hoeveel uur is de dunne kaars even lang als de dikkere kaars als je ze tegelijk aansteekt?

  3. Het gewicht van een kabelhaspel hangt af van de lengte van de kabel die er omheen gewonden is. Zo’n grote kabelhaspel bevat nieuw wel `1000` m kabel. Hij weegt dan `800` kg. Als er `200` m kabel af is, weegt de haspel met kabel nog `650` kg.
    Hoeveel weegt een lege haspel? Geef een duidelijke berekening.

Bestudeer nu:

 

www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Exponentiële groei
www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Exponentiële verbanden

 

 

Opgaven

 

  1. Door energieverbruik voor verwarming en industrie wordt CO2 (koolstofdioxide) aan de lucht toegevoegd. Stel dat elke tien jaar de uitstoot aan CO2 met 5% blijft toenemen.
    1. Waarom is hier geen sprake van lineaire groei?
    2. Met welke factor moet je de hoeveelheid CO2 elke tien jaar vermenigvuldigen?
    3. In 1990 was de uitstoot `6090` Megaton. Hoe groot zal de uitstoot in 2020 dan zijn?

  2. Een schip heeft olie op zee geloosd. De olievlek groeit elk uur ongeveer met een kwart van zijn oppervlakte. Als hij wordt ontdekt is de vlek `50000` m2 groot.
    1. Waarom is hier een tijdlang sprake van exponentiële groei?
    2. Hoeveel bedraagt de groeifactor per uur?
    3. Stel een formule op voor de oppervlakte `Opp` van de olievlek afhankelijk van de tijd `t` in uren.
    4. Teken een grafiek van de groei van de oppervlakte van de olievlek gedurende de eerste vier uur. Waarom is dit geen rechte lijn?
    5. Met hoeveel procent is deze olievlek na `3` uur gegroeid?

  3. Volgens schattingen zal de wereldbevolking de komende veertig jaar groeien van rond de `7` miljard nu (begin 2010) naar meer dan `9` miljard in 2050.
    1. Als de wereldbevolking lineair toeneemt, in welk jaar zullen er dan `11` miljard mensen op Aarde zijn?
    2. Als de wereldbevolking procentueel (exponentieel) toeneemt, in welk jaar zullen er dan naar schatting `11` miljard mensen op Aarde zijn? Gebruik eventueel een grafiek voor je schatting.

  4. Met behulp van water wordt een giftige stof uit verontreinigde grond gewassen. Een detector houdt de concentratie van de stof in het waswater bij. Die concentratie neemt met `20`% per week af.
    Na hoeveel weken is meer dan `60`% van de verontreiniging verdwenen?

 

resource.jpg

Door elkaar...

Opgaven

 

  1. Je ziet hier een viertal formules. Bij welke van deze formules is prijs recht evenredig of omgekeerd evenredig met aantal?
    1. prijs = 3,20 · aantal + 200
    2. prijs = 3,20 · aantal
    3. prijs = 200 / aantal + 3,20
    4. prijs = 200 / aantal

  2. Het cijfer van een toets wordt als volgt berekend: cijfer = punten/58 · 9 + 1.
    Het hoogste cijfer is 10, het laagste is 1.
    1. Hoeveel punten kun je maximaal halen voor deze toets?
    2. Van welk soort verband is hier sprake? Licht je antwoord toe.
    3. Welke cijfer krijg je als je 34 punten scoort?
    4. Jan rekent op een 7. Hoeveel punten moet hij dan minimaal halen?
    5. Een 5,5 of hoger wordt als voldoende gerekend. Hoeveel punten moet je daarvoor halen?
    6. De docenten die deze toets afnamen vonden achteraf de scores te laag, er waren te veel onvoldoendes. In onderling overleg werd besloten om een 5,5 toe te kennen bij een score van 20 punten.
      Voor scores onder de 20 punten werd een lineaire verdeling gebruikt. Welke formule hoort daar bij als het laagst mogelijke cijfer een 1 blijft?

  3. De wereldbevolking groeit exponentieel. De behoefte aan voedsel dus ook. Daarvoor is landbouwgrond nodig. In 1900 was de benodigde grond 450 miljoen hectare. De oppervlakte aan benodigde landbouwgrond oppNodig neemt elke tien jaar met 15% toe. Er is echter maar een beperkte hoeveelheid grond beschikbaar. De hoeveelheid beschikbare grond werd toen geschat op ongeveer 2 miljard hectare.
    1. Teken een grafiek van oppNodig waarbij de tijd loopt van 1900 tot 2100.
    2. Schat met behulp van de grafiek wanneer die grens van 2 miljard hectare wordt bereikt.
    3. Na 1980 groeide de hoeveelheid beschikbare grond oppBeschikbaar met 30 miljoen hectare per jaar. Teken een grafiek van oppBeschikbaar in dezelfde figuur.
    4. Het zal daardoor langer duren voor er een gebrek aan landbouwgrond ontstaat. Maak een nieuwe schatting hoe lang er nog voldoende landbouwgrond is.

 

resource.jpg

LogoM4Ainf.gif

Aanmelden

Ik wil mij aanmelden voor: