Lineair programmeren met OO-Calc: de Oplosser

In het rekenblad OpenOffice-Calc kun je lineair programmeren met behulp van de 'Oplosser'. Die vind je bij 'Extra'.

 

In dit practicum los je het volgende probleem op:

 

Een handelaar in fietsen, e-bikes en kinderzitjes kan deze artikelen aanschaffen bij een groothandel. Hij moet dan rekening houden met de inkoopprijs, maar ook met de opslagruimte. Verder is voor hem de winst per artikel van belang. Er gelden de volgende gegevens:     inkoopprijs (in €) opslagruimte (m2) winst per stuk (in €) fietsen 300 0,5 100 e-bikes 1200 1,0 300 kinderzitjes 36 0,1 20   Hij besluit hoogstens `100` fietsen en hoogstens `50` kinderzitjes te kopen. Hij beschikt over maximaal `101` m2 opslagruimte en over maximaal € 93.000,= om de artikelen aan te schaffen. Het gaat deze ondernemer om een zo groot mogelijke winst. Hoeveel moet hij van elk van deze artikelen aanschaffen?

 

Voor het oplossen van dit probleem kies je eerst de beslissingsvariabelen. Hier:
`x` = aantal fietsen
`y` = aantal e-bikes
`z` = aantal kinderzitjes

 

Je vindt dan in de tekst deze randvoorwaarden of restricties:

 

`300x + 1200y + 36z le 93000`
`0,5x + 1y + 0,1z le 101`
`0 le x le 100`
`0 le y`
`0 le z le 50`

 

Verder geldt als doelfunctie de totale winst: `W = 100x + 300y + 20z`.

 

Gezocht wordt een maximum van deze doelfunctie onder de beschreven randvoorwaarden.

 

Nu naar OO-Calc met het bij dit practicum horende bestand:

 

 LPfietsen.xlsx.

 

Download dit bestand en sla het op jouw computer op.
Je ziet hoe de gegevens hierboven zijn ingevoerd.
Er is een kolom "aantal" gemaakt. De cellen C4, C5 en C6 stellen de variabelen `x`, `y` en `z` voor. Vooralsnog zijn daar de waarden `0`, `0` en `0` ingevoerd.
In cel D7 zie je hoe de totale inkoopprijs wordt berekend met de XL-formule: =$D$4*x+$D$5*y+$D$6*z.
Controleer zo ook de berekeningen van de cellen E7 en F7.
De restricties gelden voor de cellen C4 (`x`), C6 (`z`), D7 (inkoop) en E7 (ruimte).
De doelfunctie zit in cel F7 (winst).
Ga dat na!

 

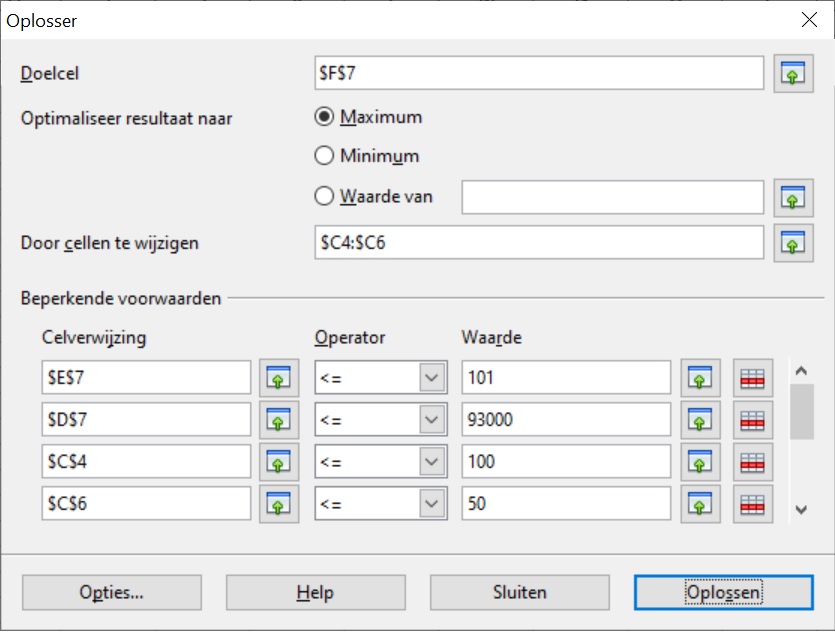
Roep nu de Oplosser op en ga als volgt te werk:

 

1. Vul achter "Doelcel" in: $F$7 (in cel F7 moet de winst komen, de dollartjes zijn bedoeld als absolute verwijzing).
2. Kies bij "Optimaliseer resultaat naar" voor: Maximum.
3. Geef de beslissingsvariabelen aan bij "Door cellen te wijzigen": $C$4 : $C$6.
4. Voeg bij "Beperkende voorwaarden" alle randvoorwaarden in. Eén daarvan is bijvoorbeeld: $C$4 < 100.
5. Voeg je alle vier de randvoorwaarden toe.
6. Tenslotte kies je voor [Oplossen].

 

Na eventjes rekenen geeft de computer aan dat hij een oplossing heeft kunnen vinden. De resultaten staan dan in de oorspronkelijke werkmap.
Ga na, dat je vindt:
`x = 80`
`y = 56`
`z = 50`
`W = 25800` als maximale winst

 

Probeer het lineair programmeren met de Oplosser goed onder de knie te krijgen met behulp van lineair programmeringsproblemen uit je wiskundeboek.

---

Math4all