Irrationale getallen

Wortels

Het is alweer zo'n 2600 jaar geleden dat de Oude Grieken de stelling van Pythagoras bewezen. Maar daarmee haalden ze een enorm probleem in huis...

Ze kenden alleen natuurlijke getallen `1`, `2`, `3`, `4`, enz. En daarnaast wisten ze dat er verhoudingen bestonden: `7//3` bijvoorbeeld als verhouding van een lijnstuk met lengte `7` en een lijnstuk met lengte `3`.

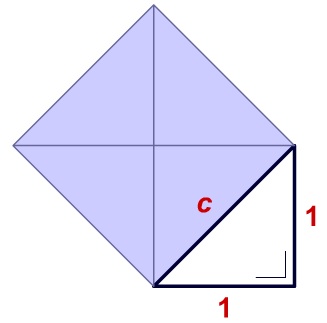
Maar neem eens een rechthoekige driehoek met rechthoekszijden van `1` cm en `1` cm. De schuine zijde (hypothenusa) is dan te berekenen uit:

`c^2 = 1^2 + 1^2 = 2`

`c` is dus een getal waarvan het kwadraat `2` is.

De kunst is nu om een getal te vinden waarvan het kwadraat `2` is. Voor de Oude Grieken bestond zo'n getal niet. Ze zochten naar de lengte van de zijde van een vierkant (kwadraat betekent vierkant) waarvan de oppervlakte `2` cm² is.

 

Tegenwoordig noem je dat getal "wortel 2" en je schrijft: `c = sqrt(2)`

Dit getal is niet een natuurlijk getal, dus moest het wel een verhouding van twee natuurlijke getallen, zijn. Iets anders was onbestaanbaar vond men in de Oudheid.
Nu alleen nog even de goede verhouding vinden...

 

 

 

De ontdekking van irrationale getallen

De Oude Grieken ontdekten dat $\sqrt{2}$  NIET als een verhouding, niet als breuk kon worden geschreven! Omdat het woord "ratio" (Latijn) zoiets als "verhouding" betekent, worden getallen die je als breuk kunt schrijven wel rationale getallen genoemd. Het getal $\sqrt{2}$ kon niet als breuk worden geschreven: het was een irrationaal getal.

Het bewijs dat $\sqrt{2}$ irrationaal is, wordt toegeschreven aan de Pythagoreërs, de volgelingen van de grote Griekse wiskundige Pythagoras. Hier volgt het bewijs:

De irrationaliteit van $\sqrt{2}$   Stel $\sqrt{2}$ is rationaal en dus te schrijven als $\sqrt{2}=\frac{p}{q}$ waarin `p` en `q` de kleinst mogelijke gehele getallen zijn.   Dan is: $2=\frac{p^2}{q^2}$ en dus `p^2 = 2q^2`. Dus `p^2` moet deelbaar zijn door `2`. Dit kan alleen als `p` deelbaar is door `2`. Dus `p = 2a`. En dan is `(2a)^2 = 2q^2`, zodat `4a^2 = 2q^2` en `q^2 = 2a^2`. Dus is ook `q^2` deelbaar door `2` en is `q` deelbaar door `2`: `q = 2b`. Maar dan is $\sqrt{2}=\frac{p}{q}=\frac{2a}{2b}=\frac{a}{b}$. Kennelijk is de breuk die $\sqrt{2}$ voorstelt dan altijd te vereenvoudigen. Maar je ging er van uit dat dit niet het geval was. Er ontstaat dus een tegenspraak. Daarom kan onze aanname dat $\sqrt{2}$ als breuk is te schrijven niet juist zijn.

Je ziet dat in dit bewijs gebruik wordt gemaakt van het feit dat als het kwadraat van een getal even is, dat getal zelf ook even is. Dit moet je dan natuurlijk wel eerst even hebben bewezen! Dat gaat zo:

 

• Een even getal `a` is een tweevoud: `a = 2n`.
  Het kwadraat is `a^2 = 4n^2` dus een viervoud.
  Het kwadraat van een even getal is altijd even.
• Een oneven getal `b` is geen tweevoud: `b = 2n + 1`.
  Het kwadraat is `b^2 = (2n + 1)^2 = 4n^2 + 4n + 1`
  en dus een viervoud `+ 1`. Het kwadraat van een oneven getal is altijd oneven.

 

Dit was voor de Oude Grieken een zeer problematische uitslag: $\sqrt{2}$  was geen rationaal getal. Zij noemden die getallen onmeetbaar en stelden ze voor als lengtes van lijnstukken. Alleen konden ze in dit geval die lengte niet in een getal of een verhouding uitdrukken!
Hun hele rekenkunde werd mede daardoor meetkundig opgebouwd...

 

 

 

Werken met onmeetbare getallen

In de Oudheid ontdekten de Grieken dat er grootheden waren die ze wel konden construeren, maar niet konden beschrijven met natuurlijke getallen. Die constructies gingen met passer en liniaal door toepassen van de stelling van Pythagoras. Maar het uitdrukken als verhouding van twee getallen bleek onmogelijk.

 

In die tijd heetten die grootheden onmeetbaar. $\sqrt{2}$  en $\sqrt{3}$  en $\sqrt{5}$  waren onmeetbare grootheden, irrationale getallen zeg je tegenwoordig.

Omdat ze wel waren te construeren kon je er mee optellen en aftrekken als met lijnstukken. En vermenigvuldigen en delen ging ook door gebruik te maken van oppervlaktes. Zo werd de hele Griekse getaltheorie een meetkundig verhaal. Geen wonder dat ze nooit negatieve getallen ontdekten...

 

Maar ze leerden zichzelf wel met wortels rekenen. De gebruikte methoden werden dan meetkundig verklaard.

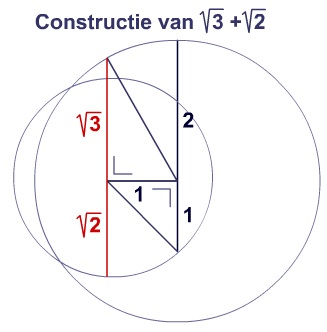
• `sqrt(2) + sqrt(3)` is meetkundig te construeren
• `sqrt(3) + sqrt(3) = 2 sqrt(3)` want het zijn twee gelijke lijnstukken, dus dan wordt de totale lengte `2` keer zo groot
• het kwadraat van `sqrt(3)` is `3`, want dat is de oppervlakte van het vierkant waarvan `sqrt(3)` de zijde is
• `sqrt(2) * sqrt(3) = sqrt(2 * 3) = sqrt(6)` wat is af te leiden uit:
  `(sqrt(2) * sqrt(3))^2 = (sqrt(2))^2 * (sqrt(3))^2 = 2 * 3 = 6`.

 

De Oudgriekse getaltheorie vind je helemaal uitgewerkt in "De Elementen" van Euklides.

 

 

 

Wortels benaderen

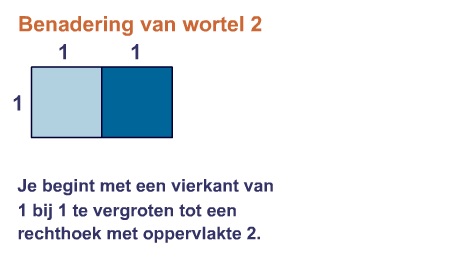
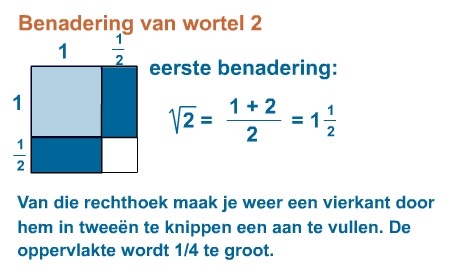
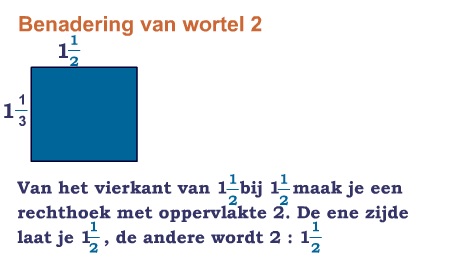
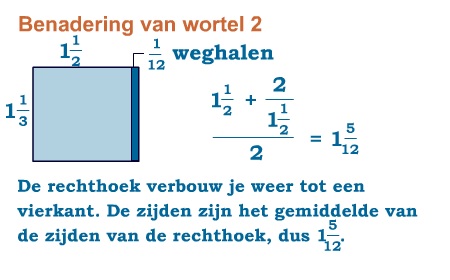
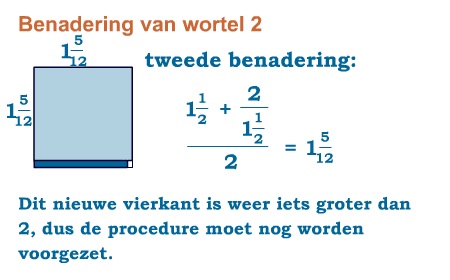
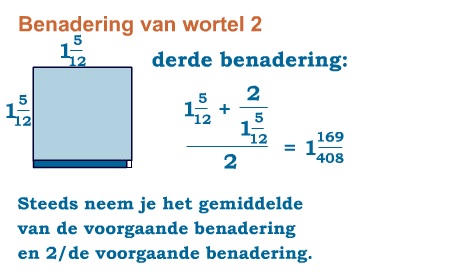
Hoewel wortels niet als breuk kunnen worden geschreven, kunnen ze wel worden benaderd met breuken. Omdat de stelling van Pythagoras al in de tijd van de Babyloniërs bekend was, bedachten die al manieren om wortels te benaderen. Bijvoorbeeld voor $\sqrt{2}$  gingen ze zo te werk:

 

 

Maar tot ver in de Middeleeuwen bleef men proberen om wortels te benaderen met breuken.
De Italiaanse wiskundige Bombelli leidde in 1572 bijvoorbeeld af dat:

 

$\sqrt{2}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{2+\mathrm{...}}}}}$

 

Deze kettingbreuk kun je oneindig ver voortzetten.
Je vindt zo redelijk snel een goede benadering.

Bombelli leidde deze kettingbreuk af door te beginnen met
`sqrt(2) = 1 + 1/y`.
Daaruit vond hij: `y = 1 + sqrt(2)`.
(Daarvoor moet je wel wat rekenen met wortels, maar het is een aardige puzzel.)
Combineren van beide leidt tot: `y = 2 + 1/y`.
En dat kun je dat weer in de beginformule invullen. Je krijgt dan het begin van de kettingbreuk, waarin je dan weer `y = 2 + 1/y` kunt invullen. Zo bouw je stap voor stap de kettingbreuk op...

 

Toen het tientallig stelsel werd ingevoerd ontstond de behoefte om wortels door decimale getallen te benaderen. Bovendien was inmiddels door de Duitse wiskundige Christoff Rudolff in 1525 het wortelteken bedacht. De tijd was rijp voor een nieuwe aanpak die pas sinds de invoering van de elektronische rekenmachine in onbruik is geraakt.

 

 

De gebruikte techniek is gebaseerd op:

`(a + b)^2 = a^2 + (2a + b)b`

Het verdelen van het getal in groepjes van twee (vanaf de komma) is nodig omdat het kwadraat van een tiental een honderdtal, van een honderdtal een tienduizendtal is, enzovoorts.
Bedenk verder zelf maar eens hoe deze techniek precies kan worden verklaard. Probeer hem bovendien maar eens uit en ontdek hoe je zelf 'slimmer' bent dan je rekenmachine!

 

Er bestaan ook andere methoden om wortels te benaderen. Bijvoorbeeld de inklemmethode.
Dan begin je met vast te stellen dat wortel `246` inligt tussen `15` en `16`.
Vervolgens bekijk je het kwadraat van `15,5`.
Dat is kleiner dan `246`, dus ligt de wortel tussen `15,5` en `16`.
Dan probeer je het gemiddelde van `15,5` en `16`.
Het kwadraat daarvan is meer dan `246`, dus... enz.

 

 

 

Wortels en machten

Wortels hebben alles te maken met kwadraten. En dus komen ze voor als oplossingen van vergelijkingen met kwadraten. Maar er zijn ook vergelijkingen waar derde machten, vierde machten en dergelijke, in voorkomen. Daarbij horen hogere machts wortels.
Bijvoorbeeld:

• `root[3](8) = 2` want `2^3 = 8`
• `root[4](2401) = 7` want `7^4 = 2401`

 

Door inklemmen kun je hogere machts wortels berekenen of benaderen. Meestal gebruik je er een rekenmachine voor.

 

Er is nog een verband tussen wortels en machten: wortels kun je schrijven als machten met gebroken exponenten. Kijk maar:

${(\sqrt[3]{8})}^3=8$ en ook ${\left(8^{\frac{1}{3}}\right)}^3=8$

Dit betekent, dat: $\sqrt[3]{8}=8^{\frac{1}{3}}$

Op deze manier is elke wortel een macht met een breuk als exponent. En zo heb je toch een manier gevonden om wortels met een breuk weer te geven.
En tussentijds heb je de irrationale getallen leren kennen...

 

 

 

---

Math4all