Fermat

De tijd van Fermat

Fermat leefde aan het einde van de Renaissance. Vooral in het Noorden van Italië waren in de veertiende en vijftiende eeuw de grote steden tot bloei gekomen en in de vijftiende en zestiende eeuw was deze 'wedergeboorte' van de klassieke cultuur over geheel West-Europa verspreid. De wiskunde had door mensen als Fibonacci, Tartaglia en Cardano in Italië en Viète in Frankrijk een nieuwe bloeiperiode doorgemaakt. Alle uit de Oudheid overgeleverde geschriften waren via het Arabisch vertaald in het Latijn en vaak zelfs in West-Europese talen onder druk van een groeiend cultureel bewustzijn.
Het Frankrijk van die jaren werd bestuurd door koning Lodewijk XIII (1610-1643) en later was daar het begin van de regeerperiode van de Zonnekoning Lodewijk XIV (1643-1715). De Nederlanden ontworstelden zich aan de Spaanse (katholieke) overheersing en kenden een periode van grote bloei. De ontdekkingsreizen vanuit Portugal, Spanje en De Nederlanden waren aan de gang of stonden voor de deur. Mensen als Galileï en Descartes voerden op meer Europees niveau de boventoon. Belangrijke wiskundigen waren Descartes, Pascal en de grote correspondent pater Mersenne die met allen contact hield. Fermat was een plaatselijke bestuurder (net als Pascal) en beoefende de wiskunde als hobby. Echte beroepswiskundigen bestonden er in feite nauwelijks, afgezien van de rekenmeesters zoals die al ruim een eeuw eerder in Noord-Italië voorkwamen. Onderwijs in de wiskunde bestond ook niet echt, geïnteresseerden lazen werk van voorgangers en vertalingen van werk van de Oude Grieken.

 

 

 

Over Fermat

Pierre Fermat werd geboren op 17 augustus 1601 in Beaumont de Lomagne waar zijn vader een welgestelde handelaar in lederwaren en bovendien viceconsul was. Pierre had een broer en twee zussen en groeide (hoogstwaarschijnlijk) in zijn geboorteplaats op. Over zijn schoolloopbaan is weinig anders bekend dan dat hij plaatsgreep in het plaatselijke Franciscaner klooster.

Fermat bezocht eerst de universiteit van Toulouse, maar verhuisde in 1620 naar Bordeaux. Daar begon hij zijn eerste wiskundige studie. In 1629 maakte hij van fragmenten van Apollonius' boek over "Meetkundige plaatsen" weer een complete versie en gaf die aan én van de wiskundigen daar. Ook werkte hij er aan het berekenen van maxima en minima.
Vanuit Bordeaux vertrok Fermat naar Orléans. Daar studeerde hij af in de rechten en hij werd benoemd als raadsheer van het parlement in Toulouse. Vanaf 14 mei 1631 was hij advocaat en raadsheer in Toulouse en veranderde hij zijn naam in Pierre de Fermat. De rest van zijn leven zou hij in Toulouse wonen. Hij werkte afwisselend daar en in zijn geboortestad, carrière makend in het starfhof van Toulouse. In 1653 overleefde hij er zelfs de pest, hoewel zijn dood op zeker moment werd aangenomen. Hij stierf er op 12 januari 1665.

 

Fermat's grote hobby was de wiskunde. Hij ontmoette in Toulouse een gelijkgestemde collega die Carcavi heette en vertelde hem over zijn passie en zijn werk. Carcavi vertrok in 1636 naar Parijs om te gaan werken in de Koninklijke Bibliotheek en maakte daar contact met Marin Mersenne en de groep wiskundigen om deze priester-wiskundige heen. Mersenne hield in die tijd met de belangrijkste wiskundigen een briefwisseling en begon ook met Fermat te corresponderen. Fermat vertelde Mersenne over zijn werk op het gebied van vallende lichamen (hij meende dat Galileï fouten had gemaakt in zijn beschrijving van de vrije val) en op het gebied van spiralen en zijn reconstructie van het geschrift van Apollonius.
Fermat was echter maar matig in de natuurkunde en de toepassing van zijn wiskundige methoden geïnteresseerd, liever werkte hij aan zuiver wiskundige bewijzen. In én van zijn eerste brieven aan Mersenne schreef hij over twee problemen op het gebied van het berekenen van maxima en/of minima. Daarin gebruikte hij zijn karakteristieke werkwijze: anderen uitdagen om te bewijzen wat hij zelf al had gevonden.

 

Roberval en Mersenne ontdekten dat Fermat zich met voor die tijd buitengewoon lastige vraagstukken bezig hield en verzochten hem zijn methoden te publiceren. Daarop stuurde hij hen zijn aanpak van het berekenen van maxima en minima en raaklijnen aan krommen, zijn algebraïsche benadering van de meetkunde (de grondslagen van de analytische meetkunde) en zijn gereconstrueerde tekst van Apollonius. Zijn reputatie als groot wiskundige werd er door versterkt, maar tot een daadwerkelijke uitgave van zijn werk kwam het echter niet. Fermat werkte zijn ideeën namelijk zelden helemaal uit. Bovendien gebruikte hij de inmiddels ietwat verouderde notaties van Viète, waardoor zijn geschriften niet erg pasten in de modernere ontwikkelingen ingezet door Descartes.

Wel raakte Fermat in conflict met Descartes. Fermat bekritiseerde namelijk Descartes' bewijs van de brekingswet van licht. Bovendien leken zijn methoden voor het berekenen van maxima, mininima een raaklijnen totaal anders dan de rekenmethoden van Descartes in 'La Géométrie'. Descartes viel daarop Fermat's technieken aan en er ontbrandde een pittige strijd, die uiteindelijk door Fermat werd gewonnen, zoals ook Descartes uiteindelijk toegaf. Toch bleef de laatste Fermat's werk in brieven aan Mersenne kleineren en omdat Descartes al een sterke reputatie had, deed dit Fermat's aanzien geen goed.

 

Van 1643 tot 1654 was Fermat niet in staat om contact te houden met zijn collega's in Parijs. Ten eerste was hij te druk met zijn gewone werk zodat de wiskunde er bij in schoot. Maar bovendien was er in die tijd in Frankrijk een burgeroorlog gaande (de 'Fronde') en werd in 1651 Toulouse door de pest getroffen. Fermat overleefde deze ziekte zelf ternauwernood. In die tijd werkte Fermat aan de getallentheorie en formuleerde hij zijn beroemde stelling die later als de 'Laatste Stelling van Fermat' de wiskundige wereld honderden jaren bezighield. Hij schreef in de kantlijn van Brachet's vertaling van Diophantos' "Arthmetica" dat

$x^n+y^n=z^n$

geen positieve gehele oplossingen heeft voor $x$, $y$ en $z$ als $n>2$. (Het geval $n=2$ slaat op de stelling van Pythagoras.)
Fermat schreef dat hij daarvoor een heel opmerkelijk bewijs had gevonden, waarvoor de kantlijn echter net te weinig ruimte bood. Diverse wiskundigen hebben daarna geprobeerd om een bewijs voor deze stelling te vinden, hetgeen heeft geleid tot veel ontdekkingen in de getallentheorie en de algebra. Pas in 1994 is Andrew Wiles erin geslaagd om een algemeen aanvaard bewijs te leveren.

 

In 1654 begon Fermat weer te schrijven, nu met Blaise Pascal die hem vroeg om een oordeel over zijn ideeën op het gebied van een aantal kansvraagstukken die hij voor zijn neus had gekregen. Pascal kende Fermat via zijn (drie jaar daarvoor overleden) vader Etienne Pascal en wist van zijn grote wiskundige vaardigheid. Uit deze correspondentie ontstond de kansrekening als wiskundige theorie.
Fermat poogde echter de briefwisseling ook naar andere terreinen van de wiskunde te verleggen, met name de getallentheorie. Hij vond echter weinig gehoor omdat daarin maar weinig andere wiskundigen waren geïnteresseerd.

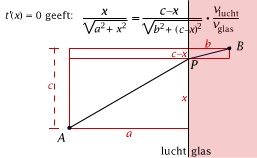
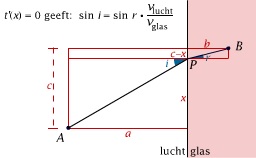
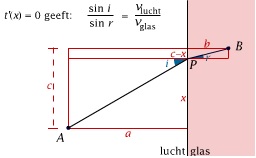
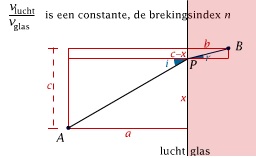
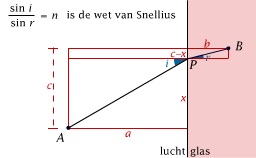
Hij werd echter door een student van Descartes om hulp gevraagd omtrent hun correspondentie over de eigenschappen van licht en met name de breking van licht bij de overgang naar een ander medium. Fermat bekeek zijn bezwaren tegen Descartes' optica nog eens en bedacht het principe van de kortste weg. Daarmee vond hij een elegant bewijs van de brekingswet van Snellius (die Descartes en Snell al eerder hadden gevonden, maar waarvoor zij een nogal ingewikkelde verklaring bezigden). Hoewel Fermat hiermee niet onmiddellijk de wereld der wetenschap wist te overtuigen, is het tegenwoordig een belangrijk grondprincipe in de natuurkunde.

 

In 1656 begon Fermat met Christiaan Huygens te corresponderen. Eerst met name over de kansrekening, waarin Huygens toentertijd was geïnteresseerd, maar later schreef Fermat ook veel over zijn methoden in de getallentheorie. Ook nu vond Fermat echter maar weinig gehoor.
En dat lijkt wel zijn voortdurende lot te zijn: hij was het meest geïnteresseerd in de getallenleer, maar vond daarin geen medeliefhebbers van gelijkwaardig niveau.

Fermat overleed in 1665.

 

 

 

Fermat's belangrijkste werk

Behalve een paar losse geschriften en veel brieven publiceerde Fermat geen systematische uitleg van zijn gedachten. Een paar van de meest opvallende resultaten werden na zijn dood gevonden op losse papiertjes of in de kantlijn van boeken van anderen die hij bestudeerde, vrijwel altijd zonder bewijzen van zijn stellingen. Hij was waarschijnlijk te bescheiden en teruggetrokken om zich in te spannen om zijn werk in druk te zien. Fermat hield zich op het gebied van de wiskunde bezig met:

 

Grondslagen van de analytische meetkunde

Het lijkt er op dat hij het principe van het toepassen van algebra (werken met variabelen) op meetkundige problemen had doordacht voor het lezen de Descartes' "Géométrie". Hij gebruikte echter nog notaties zoals Viète had gedaan en vond daarom maar weinig gehoor. Het principe van 'vergelijkingen van krommen' was hem echter bekend.
Daarna lijkt hij zich vooral te hebben beziggehouden met het berekenen van raaklijnen, van oppervlaktes onder krommen en het berekenen van maxima en minima. Onder andere vond hij de oppervlakte ingesloten door een parabool en een lijn en door een hyperbool en een lijn. Ook hield hij zich bezig met het berekenen van het 'Fermat-punt' in een driehoek, dat is het punt waarvan de som van de afstanden tot elk der hoekpunten het kleinst is. Waarschijnlijk werd hij daartoe geïnspireerd door het lezen van werk van Cavalieri en Wallis.

 

Getallentheorie

Dit was Fermat's favoriete onderwerp. Hij werkte aan een heruitgave van het werk van Diophantos en de notities en commentaren daarbij bevatten diverse zeer elegante stellingen. Voorbeelden van resultaten van Fermat op dit gebied zijn:

Elk priemgetal groter dan 2 kan op precies én manier worden geschreven als het verschil van de kwadraten van twee gehele getallen. Fermat's bewijs: Neem aan dat $p$ een priemgetal is en stel dat het gelijk is aan $x^2-y^2=\left(x+y\right)\left(x-y\right)$. Omdat $p$ alleen deelbaar is door $1$ en door $\mathrm{p}$ moet $x+y=p$ en $x-y=1$. Daaruit vind je precies én oplossing voor $x$ en $y$.

Hij bewees Diophantos' stelling dat de som van de kwadraten van twee gehele getallen nooit kan worden geschreven als $4n-1$, waarin $n$ een geheel getal boven $0$ is.

Elk priemgetal van de vorm $4n+1$ ( $n$ geheel en boven $0$) kan op precies én manier worden geschreven als de som van twee kwadraten. Het bewijs werd later geleverd door Euler.

Als $a$, $b$ en $c$ gehele getallen zijn waarvoor geldt $a^2+b^2=c^2$, dan kan $ab$ geen kwadraat zijn. Een bewijs werd later geleverd door Lagrange.

De beroemde "Laatste stelling van Fermat", die zo genoemd werd omdat het de laatste was waarvoor (in 1994) een bewijs werd gevonden: Er bestaan geen gehele getallen $x$, $y$ en $z$ waarvoor $x^n+y^n=z^n$ als $n>2$. Fermat zelf kon waarschijnlijk wel de speciale gevallen voor $n=3$ en $n=4$ bewijzen, hoewel die bewijzen niet zijn teruggevonden maar later zijn gerecontrueerd door Euler. Veel later vonden andere wiskundigen bewijzen voor andere speciale gevallen, maar het duurde tot 1994 voordat Andrew Wiles een bewijs voor de algemene stelling vond.

De grondbeginselen van de kansrekening:

Pascal kreeg een probleem op het gebied van de kansrekening voorgelegd en vroeg Fermat om zijn oplossing te bekijken. Daarop ontstond een briefwisseling over kansrekenen die de grondslag vormde voor het ontstaan van kansrekening als wiskundige theorie.

 

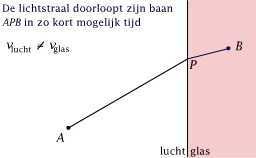
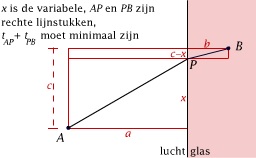
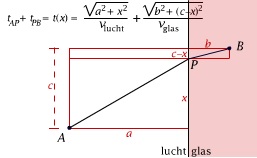
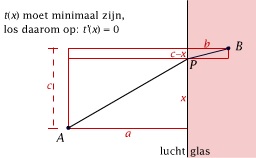
Het principe van de kortste weg in de optica

In deze animatie zie je hoe het principe van Fermat (zoals het ook wel wordt genoemd), leidt tot de bekende brekingswet van Snellius (de wet die door de Nederlandse wetenschapper Snell werd geformuleerd).

 

 

 

---

Math4all