Meetkunde

Waar gaat het over?

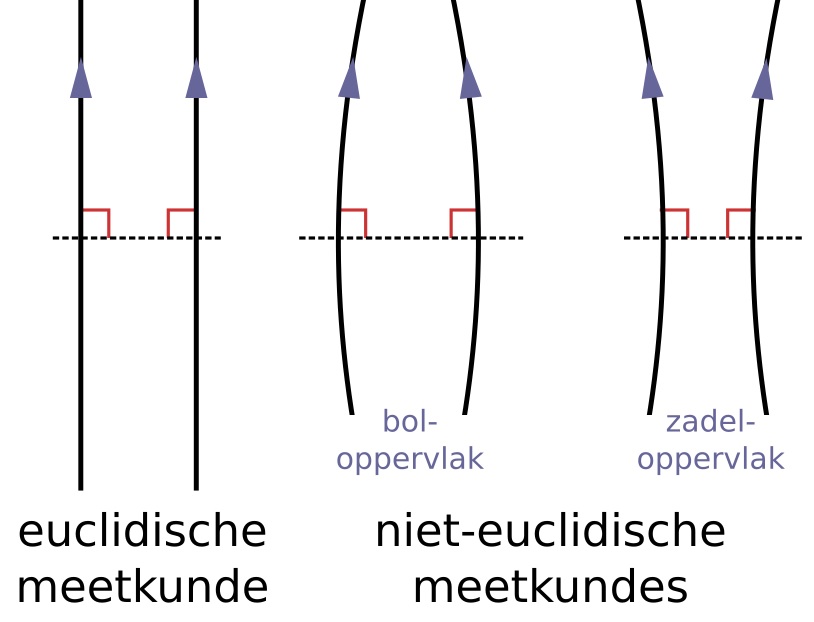
Over het beschrijven van vormen en afmetingen in de ruimte om ons heen. In het begin denken mensen op een platte wereld te wonen met drie dimensies. Daarop is de euclidische meetkunde dan ook gebaseerd. Pas als de mensheid ontdekt dat ze op een bol woont en daarop metingen wil uitvoeren, ontstaan er niet-euclidische meetkunden.

Hoe werkt het?

Om vormen en hun afmetingen te kunnen beschrijven zijn afspraken nodig over wat een punt, een lijn, evenwijdigheid, etc., is. De euclidische meetkunde kent naast een aantal basisaannames vijf axioma's. Daarop zijn alle verdere stellingen gebaseerd en gevormd tot één theorie.
Na de invoering van het coördinatenstelsel ontstond de analytische meetkunde die is gebaseerd op de euclidische meetkunde, waarbij objecten algebraïsch worden beschreven.
En dan is er de niet-euclidische meetkunde waarin het axioma dat er door een punt buiten een lijn precies één lijn evenwijdig aan die lijn bestaat, ongeldig is.
Tegenwoordig zijn wiskundigen met meerdimensionale meetkunde, meetkunde van oprekbare oppervlakken, en dergelijke bezig.

Wie en wanneer?

De meetkunde is vele duizenden jaren oud. De eerste die er een theorie van maakte (omstreeks 300 v.Chr) met definities, axioma's en bewezen stellingen is Euclides in zijn wereldberoemde boek "De elementen". Dit is eeuwenlang hèt wiskundeboek geweest.

De naam "meetkunde" (NL) is rond 1600 door Simon Stevin bedacht. En de analytische meetkunde ontstond iets later vanuit het werk van René Descartes.

Na 1800 ontstond onder invloed van landmeetkunde op het aardoppervlak de niet-euclidische meetkunde. Bekende namen zijn Gauss, Bolya en Lobachevsky.
Nog later ontstond de ruimte-tijd-meetkunde (4 dimensies) en andere meerdimensionale meetkunden. En dan heb je nog de topologie (meetkunde van oprekbare oppervlakken) en ...