Bolmeetkunde

Waat gaat het over?

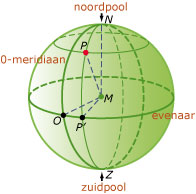
Je positie op een bol (zoals de Aarde) beschrijf je met een bijzonder assenstelsel. De doorsnede van de bol met een vlak door het middelpunt $M$ is de evenaar. De lijn door $M$ loodrecht op dat vlak snijdt de bol in de twee polen. De oorsprong is het snijpunt van de evenaar en een daar loodrecht opstaande meridiaan, de 0-meridiaan. Heb je een punt $P$ vastgelegd, dan kun je kijken naar verplaatsingen, lijnstukken, driehoeken, ...

Hoe werkt het?

De plek van $P$ wordt bepaald door $\angle OMP\text{'}$ (lengtegraad, meridiaan) en $\angle P\text{'}MP$ (breedtegraad). Bijvoorbeeld $P=\left({10}^{\circ }OL,{60}^{\circ }NB\right)$ dus `10` graden oosterlengte en `60` graden noorderbreedte. De kortste verbinding tussen $A\left(0^{\circ },{60}^{\circ }NB\right)$ en $B\left({60}^{\circ }OL,0^{\circ }\right)$ is een stuk van een grootcirkel op de bol.
De hoeken van $△ONB$ zijn samen ${90}^{\circ }+{90}^{\circ }+{60}^{\circ }>{180}^{\circ }$.
En hoe zit het met evenwijdigheid op een bol? Hier begint de niet-euclidische meetkunde...

Wie en wanneer?

Euklides (ca 300 v.Chr.) bouwde in De Elementen de hele meetkunde op vanuit vijf axioma's. Het vijfde, dat over evenwijdigheid, geldt op een bol niet. Bolmeetkunde is een niet-euclidische meetkunde. Op een bol is de hoekensom van een driehoek groter dan ${180}^{\circ }$, etc.
In de Oudheid werd de eerste bolmeetkunde ontwikkeld door astronomen die naar de "hemelkoepel" keken, een "bol" waarover sterren, planeten, bewogen. Bolmeetkunde werd vooral van belang toen in de 16e eeuw navigatie over de wereldzeeën en later de landmeetkunde ontstonden. Er is in die tijd dan ook een enorme ontwikkeling zichtbaar waarbij de goniometrie de hoofdrol speelt.