Gelijkvormigheid

Waar gaat het over?

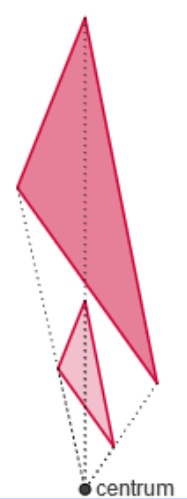
Figuren zijn gelijkvormig als de éne figuur een vergroting is van de andere (en dus de andere een verkleining van de éne). Er is dan een punt van waaruit je figuur I kunt vermenigvuldigen tot figuur II. De bijbehorende vergrotingsfactor noem je vaak $k$. Alle bij elkaar passen lengtes hebben dan dezelfde verhouding.

Hoe werkt het?

Van een cocktailglas heeft de bovenkant een wijde kegelvorm. Dat heeft een goede reden. Stel dat de vloeistofspiegel van de cocktail tot halverwege de hoogte van de kegel staat, dan is de hoogte van de vloeistofkegel precies $\mathrm{0,5}$ keer die van de hele kegel. Maar bij een vergroting met factor $\mathrm{0,5}$ wordt een inhoud dan met $\mathrm{0,5}\cdot \mathrm{0,5}\cdot \mathrm{0,5}=\mathrm{0,125}$ vermenigvuldigd.
De cocktail beslaat maar $\mathrm{12,5}$% van de inhoud van het glas...

Zo worden bij vergroting (of verkleining) met factor `k` alle lengtes `k` keer, alle oppervlaktes `k^2` keer en alle volumes `k^3` keer zo groot (klein).

Wie en wanneer?

Euklides (ca 300 v.Chr.) bouwde in De Elementen veel van zijn theorie op met behulp van gelijkvormigheid. Voor hem waren getallen lengtes van lijnstukken die je kon vergroten en verkleinen en waarvan je met de verhoudingen kunt werken.
Eén van de mooiste verhoudingen is de Gulden snede.
En wat denk je van dit soort figuren, die fractalen heten? Veel gelijkvormigheid...